fluorF's Laboratory

어쩌다가 우연히 듣게 된 3년 전 이 노래에 완전히 꽂힌 결과 비록 힙합에 대해 아는 것이 없으나  매우 인상깊게 들은 곡이라 홈페이지에 이에 관한 짧은 글까지 싣게 되었다.

누구라도 이 곡을 들으면 고급지면서도 몽롱한 그런 느낌을 받게 될 것이라고 생각한다. 물론 가사에 등장하는 사람들부터 심상치 않다. 살바도르 달리(Salvador Dali), 판 호흐(Van Gogh), 파블로 피카소(Pablo Picasso), 그리고 폴 고갱(Paul Gauguin)같은 유명한 화가 이름들이 등장하는 랩 음악을 들어본 적이 있는가? 당장 여기에서부터 청자(聽者)들은 들어본 적 있는, 뭔가 유명하긴 한데 자세히는 잘 모르는 사람들의 위대한 서양 사람들의 이름들을 들으며 뭔가 고급지다고 느낄만도 하다. (왜 이런 외국인 이름 늘어놓는 것에 고급스러움을 느껴야 하는 것인지 비판 의식을 가지고 싶긴 하지만, 일단 대중의 일반적인 감성이 그러하므로 넘어가자.) 물론 여기서 가장 중요한 건 '들어본 적 있는' 사람이라는 뜻이다. 만일 저 사람들 이름 대신 힐베르트, 칸토어, 푸앵카레 뭐 이런 이름을 집어넣는다든지 플랑크, 하이젠베르크, 슈뢰딩거 이런 이름을 가사에 썼다면 청자들의 외면을 받았을 것이다.

라임도 굉장히 재미있는데 가장 인상깊었던 부분은 'identity'와 '알겠지'였다. 억지 아니냐고 생각할 수도 있겠지만, 'identity'라는 단어를 봤을 때 [아이덴티티]라는 상상 속의 발음기호를 떠올린다든지 '알겠지'를 'algetji'라고 로마자화 하는 사람들이라면 이 두 단어를 어절 단위의 라임으로 처리하려는 생각조차 해 본 적이 없었을 것이다. 게다가 '퍼졌지', '몽롱해'라는 가사에서 일부러 마이크 효과를 주어 목소리가 퍼져나가는 듯한 효과를 주는 것도 굉장히 흥미로웠다. 비록 이런 것은 소소한 효과이지만 노래가 미술과 관련된 비유 및 이야기를 굉장히 많이 사용하고 있어서 그런지 붓터치를 통해 대상의 양감과 질감을 추가적으로 표현하는 회화적 기법이 노래에 적용된 것같은 느낌을 받았다.

하지만 이 곡에서 가장 인상적인 것은 바로 곡의 전반을 주름잡는 음계(scale)이다. 아래는 악보나라에서 제공하는 후렴구 악보 샘플이다.

조표에 내림표(♭)가 네 개가 있으므로 소시적에 피아노를 좀 두들겨 본 사람이라면 이 곡은 내림 가장조(A♭ major)이거나 바단조(F minor)일 것이라는 예측을 쉽게 해 볼 수 있을 것이다. 내림 가장조와 바단조의 음계를 혹 모르는 분들을 위해 아래에 그림을 연결시켜 놓았다.

자, 그렇다면 빈지노의 'Dali, Van, Picasso'의 주음계는 무엇일까? 내림 가장조? 바단조? 여기서부터 사람들은 헛갈리기 시작할 것이다. 우선 내림 가장조는 확실히 아니다. 보통 장조는 밝고 명랑한 기분으로 시작하고 끝나는 것이 일반적이다. 그런데 바단조라고 말하기에도 뭔가 애매한 것이, 단조 곡은 뭔가 슬퍼야 하지 않는가? 이 곡은 분명 장조는 아닌데 그렇다고 단조라고 하기엔 다소 덜 슬프다(?)는 것이 문제이다.

코드 분석을 해 보면 이야기는 더욱 황당해진다. 일단 장조는 확실히 아니니까 바단조, 그것도 자연 단음계, 즉 F natural minor라고 가정해놓고 분석을 진행해보자. 아래는 바단조의 다이어토닉 스케일(diatonic scale, 온음계)에서 각 음을 제1음으로 하여 제3음과 제5음을 쌓아 올린 다이어토닉 3화음(triad)을 나타낸 그림이다.

자연 단음계의 다이어토닉 3화음은 악보 아래에 있는 로마자의 표시를 참조할 수 있는데, 정확히 표현하자면 Im, II˚, ♭III, ♭IVm, Vm, ♭VI, ♭VII 가 된다. (참고로 ˚ 표시는 디미니쉬 코드를 말한다.) 그럼 이제 빈지노의 악보로 옮겨가서 확인해보자. 스크롤이 귀찮은 당신을 위해 여기에 써두겠다.

B♭m9     C7+11  |  B♭m9     C7+11  |  B♭m9     C7+11  |  A♭aug+7/E     (Fm)    |

사실 단순하게 저것들의 반복이다.

첫 코드인 B♭m9는 ♭IVm에 텐션 노트(tension note)로 9음이 붙은 것이니 OK. 그런데 당장 다음에 등장하는 C7+11 ― C7(#11) 이라고도 쓸 수 있다. ― 코드부터 엉망이다. 바단조에서 이 코드는 V7로 도미넌트 세븐스 코드(dominant seventh chord, 속7화음)이 되는데 이 코드는 자연 단음계 다이어토닉 코드에서 찾아볼 수 없는 코드이다. 자연 단음계에 따르면 제5음을 근음으로 하는 다이어토닉 코드는 무조건 단화음(minor chord)이어야 하는데 말이다. 더 큰 문제는 이게 변칙적으로 잠깐 사용된 화음이 아니라 계속 반복된다는 것. 마지막 마디에 등장하는 A♭aug+7 코드는 그야말로 재앙이다. 바단조에서 이 코드는 ♭III+ 인데 역시 자연 단음계 다이어토닉 코드에서는 찾아볼 수 없는 코드이다.

게다가 꼭 그래야만 하는 것은 아니지만 대체로 주음계의 주요한 구성요소가 포함된 으뜸화음(tonic chord)의 구성요소는 곡 첫 마디에 항상 등장하게 마련이다. 그래야 '우리 곡은 이 음계로 구성된 곡이야'라는 음악적 암시를 청자들에게 안정적으로 줄 수 있기 때문이다. 그러나 불행히도 이 곡의 전반을 책임지는  |  B♭m9     C7+11  |  에서는 바단조의 향기를 도저히 느낄 수가 없다. 따라서 우리는 여기서 이 곡의 주음계가 바단조조차 아니라는 확신을 갖게 된다.

도저히 이해가 안 가는 코드를 뒤로 한채 후렴구의 멜로디를 살펴보자. 멜로디는 굉장히 단순하고 일견 코드와는 달리 바단조 음계의 음을 이탈(?) 없이 바르게 사용하고 있는 것처럼 보인다. 그런데 여기에서도 뭔가 석연치 않은 부분이 있다. 멜로디를 잘 살펴보면 악절의 마지막인 '왔어', 'Picasso' 가 종지(cadence)로서 F음에 실린 것을 제외하고는 대체로 왠지 C음(도)을 기준으로 한 선율같다는 인상을 받게 된다. 'Dali', '같이', 'body', 'artist'가 모두 길이가 긴 C음으로 유지되는 것도 그러하고 그 다음에 이어지는 'Dali, Van, Picasso를 보며 난 자랐어'와 같은 선율은 C 단음계에서나 등장할 법한 선율이기 때문이다.

그렇다면 도대체 이 곡은 무엇이란 말인가? 흥분을 가라앉히고 한번 천천히 시도를 해보자. 우선 C음을 기준으로 한 선율같다는 느낌적인 느낌을 받아들이고, 내림표 네 개를 조표를 기억한 상태에서 C음부터 차근차근히 7개의 음을 쌓아나가보자. C 다음은 ♭D, 그 다음은 ♭E, ... 이런 식으로 말이다. 그러면 아래와 같은 음계가 탄생한다.

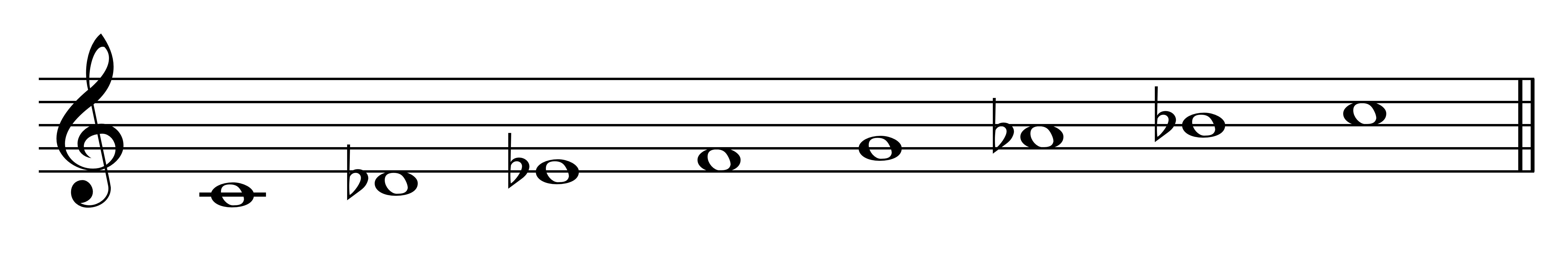
이 음계는 기존의 장단조와는 크게 다르다. 장조는 3-4음, 7-8음 사이가 반음이며 존재하며 나머지는 모두 온음 차이이다. 이에 반해 단조는 2-3음, 5-6음 사이가 반음이다. 그런데 이 새로운 음계는 무엇이란 말인가? 1-2음, 5-6음 사이가 반음이다. 일단 2개의 반음과 5개의 온음이 있으니 얘도 다이어토닉 음계인 것은 맞다. 그렇다면 이것은 장단조의 확장판이라고 봐야 하는가?

사실 관계는 반대이다. 장단조의 확장판인 것같은 이 음계가 사실은 일반적인 음계이고, 그 일반적인 음계들 사이에 장조와 단조가 존재하는 것이다. 우리는 이 '일반적인 음계'를 가리켜 선법(旋法, mode)이라고 한다. 선법에 대한 자세한 설명은 추후 글 목록에서 업로드할 음악 관련 글에 싣는 것으로 대신하려고 한다. (비록 언제 업로드될 지는 기약이 없으나...) 선법의 정의에 따라 위에 그려진 음계를 나타내는 명칭은 바로 다 프리지언(C Phrygian)이다. 피아노가 있다면 저 음계를 차례차례 눌러보라. 장조도 아닌 것이 단조도 아닌 것이 굉장히 기묘하게 들린다. 따라서 빈지노의 'Dali, Van, Picasso'는 내림 가장조도, 바단조도 아닌 다 프리지언이라는 것이다. (참고로 이걸 C 프리지언이라고 쓰고 싶으나 앞에서 한국어로 조를 표기한다는 규칙을 세워 계속 써왔으므로 계속 '다 프리지언'이라고 굉장히 어색하게 눈물을 머금고 쓴다.)

그러나 여기에도 문제가 있다. 다 프리지언에서는 아까 코드 분석에서 등장한 C7+11,  A♭aug+7가 만들어질 수 없다는 문제가 있다. 물론 멜로디만 따지면 다 프리지언이라고 주장해도 아무 문제가 없지만, 코드를 따져보면 이것은 덮어놓고 프리지언이라고 주장할 수 없는 문제임을 알게 된다. 아, 어쩌란 말인가, 이제 답이 없구나 느껴질 찰나 이 두 코드에 공통적인 '문제'가 있다는 것을 예리하게 집어낼 수 있다면 당신은 희망을 발견한 것이다. 다 프리지언에서 이 두 코드를 만들 수 없는 이유는 순전히 제3음이 E가 아닌 E♭이다. 그렇다면 이젠 선법 음계도 포기하고 눈 한번 딱 감고 과감한 짓을 저질러보자: 제3음을 반음 올려 E로 만들어 아래와 같이 음계를 구성해보자.

이 음계는 더 이상 다이어토닉 음계가 아니다. 왜냐하면 2-3음 사이가 온음 반(1.5)의 차이가 나기 때문이다. 그런데 우리는 이런 식으로 1.5음 차이가 나는 음계를 중학교 음악 시간에 배운 적이 있었다. 그게 무엇이냐하면 바로 화성 단음계(harmonic minor scale)이다. 아래는 바단조 화성 단음계(F harmonic minor)의 음계 구성이다.

화성 단음계에서는 제7음을 반음 올려 단조의 5도 화음이 딸림화음(dominant chord)의 속성을 가지도록 조절된 것이다. 그런데 눈치가 빠른 사람은 이 바단조 화성 단음계와 저 위에 있는 다이어토닉 음계가 아닌 음계 사이에 모종의 관계가 있음을 바로 알아차릴 수 있을 것이다. 이 둘은 마치 다장조와 가단조의 관계처럼 구성음은 완벽하게 똑같지만 음계가 시작되는 근음(root)만 다르다. 쉽게 말해 음의 순서(F, G, A♭, B♭, C, D♭, E, F)만 바꿔서 C부터 시작하게 만들어놓으면 (C, D♭, E, F, G, A♭, B♭, C) 위의 음계가 만들어진다. 단, 관계조(related key)인 다장조와 가단조는 근음 사이에 서로 단3도(C-A) 차이가 있는데 비해, 이 두 음계는 서로 완전5도(F-C) 차이가 난다. 이런 이유로 위에서 봤던 음계를 다음과 같이 부른다.

C harmonic minor perfect fifth below (C Hmp5↓)

우리말로 하면 '다 화성 단음계 하(下) 완전 5도' 정도 되려나? 그래서 어느 누구도 이것을 우리말로 부르지 않고 차라리 '씨 하모닉 마이나 퍼펙트 피프쓰 빌로우'라고 부른다. 이런들 어떠하고 저런들 어떠하리. 아무튼 이런 식의 접근을 통해 우리는 뭔가 답에 가까운 것을 찾았다. 빈지노의 'Dali, Van, Picasso'를 구성하는 음계에는 바로 C Hmp5↓ 가 있다. 참고로 이 음계는 프리지언 도미넌트(Phrygian dominant)라고도 부르는데 집시 음악에서 들릴 것 같은 굉장히 이국적이고도 독특한 음계이다.

여기서 한 가지 더 고려할 것이 있다. 멜로디에서 등장하는 E♭는 C Hmp5↓ 음계의 구성음이 아닌데 이를 어떻게 설명할 수 있냐는 것이다. 우선 다장조 곡이라고 해서 멜로디를 구성할 때 흰 건반만 사용하는 것은 아니듯 C Hmp5↓ 음계에서도 꼭 일곱 음만 사용해서 멜로디를 만들어야 하는 원칙같은 건 없다.  또한 E♭음이 등장하는 가락은 모두 C7+11 코드의 지배를 받는데, E♭는 해당 코드의 증9음(#9)에 해당하며 딸림화음이 가질 수 있는 텐션에 포함되므로 크게 어색하지 않은 경과음(passing note)의 역할을 해낼 수 있는 것이다. 이런 측면에서 본다면 C Hmp5↓ 음계의 멜로디에서 중간중간 E♭가 등장하는 것도 무리는 아니다. 사족이지만, 이 음은 마치 F음에 대롱대롱 매달린 채 끌려오는 듯한 방식으로 연주된다. 즉, F음에 비해 코드 진행 및 가락 구성에 아주 큰 영향을 줄만큼 큰 음은 아니라는 의미라고 볼 수 있겠다. (실제로 F-E♭-F-E♭의 가락을 그냥 F-F로 불러도 어색하지 않다.)

마지막으로 가장 중요한 문제가 남아 있다. 애초에 이 곡의 주음계가 C Hmp5↓ 가 아닌 바단조 화성 단음계인 것이 아니었냐는 질문이 있을 수 있다. 사실 장단조와 선법을 아우르는 다이어토닉 음계와 비(非)다이어토닉 음계를 순차적으로 설명하기 위해 이 글에서는 빙빙 돌아가는 사고의 흐름 혹은 비틀기를 구사해냈지만, 사실 바단조 자연 단음계가 아닌 상태에서 E 음이 쓰이는 걸 봤다면 누구나가 화성 단음계를 바로 떠올렸을 것이다. 바단조 화성 단음계를 기반으로 해서 코드 분석을 하면 |  B♭m9     C7+11  |  는 단음계 버금딸림화음(SDm)과 딸림화음(D)으로 이어지는 안정적인 코드 진행이 되고, 전체 곡을 바단조 화성 단음계로 이해해도 전혀 무리가 없다. 하지만 여전히 멜로디 라인에서 C 음에 무게가 실리는것 같은 느낌적인 느낌을 지울 수는 없다. 그래서 나는 이 곡 'Dali, Van, Picasso'가 바단조 화성 단음계와 C Hmp5↓를 모호하게 얼버무렸다고 양보를 하면서도 C Hmp5↓ 로 해석하는 것이 이 곡의 불안정성 혹은 묘한 분위기를 설명하는 데 훨씬 더 바람직하다고 생각한다.

그런데 이런 모호함을 떨쳐버리고 하나의 음계를 단적으로 지향하는 지점들은 악보상 악절들의 마지막 마디들에 있다. 특히 '여기까지 "왔어"' 부분과 'I'm Dali, Van, "Picasso"' 부분의 큰따옴표 친 부분이다. 이 가사에 해당하는 음은 F음인데 이것은 바단조 단음계의 근음이다. 게다가 이 음을 지배하는 마지막 마디 코드는 A♭aug+7/E 혹은 A♭aug+7/F 인데 단음계의 제3도 화음은 으뜸화음(Tm)의 성격을 가진 화음이기 때문에 끝나면서 소위 거짓 종지(deceptive cadence)가 이뤄지게 된다. 또한 이 다음에 이어지는 코드는 Fm 코드가 등장하는데 이것은 바단조 단음계의 으뜸화음이다. 결국 실컷 모호한  C Hmp5↓ 코드와 멜로디 라인으로 한껏 청자들의 귀를 흩뜨려 놓은 다음 후렴이 끝나는 부분들은 명확하게 바단조 화성단음계 으뜸화음을 펼침으로써 안정적으로 한 단락이 끝났음을 음악적으로 명시하는 것이다. 그래서 이 노래를 듣다보면 '여기까지 왔어' 혹은 'I'm Dali, Van, Picasso' 부분에 이르러서는 그간의 몽롱한 모호함이 좀 걷히고 '자, 이제 그 다음은 어떤 랩이 펼쳐지나?'라는 생각을 하게 되는 것이다.

이런 harmonic minor perfect fifth below 혹은 프리지언 도미넌트 음계가 쓰인 대중 가요가 예전에도 발표된 적이 있었다. 바로 f(x)의 '첫 사랑니(Rum Pum Pum Pum)'이다. 자세한 내용은 Weiv에 실린 글을 참조! 이 노래에서도 '안녕 한번쯤은 날 들어 봤겠지'는 B Hmp5↓ 로 진행하다가 '너의 사랑니'는 나단조로 진행하여 다음 멤버에게 노래 마이크를 넘겨준다. 즉, 전곡을 Hmp5↓ 로만 구성해서는 안정감도 없고 계속 불안하게 묘한 느낌만 겉돌게 되니까 노래의 구성 요소들이 끝나는 지점마다 이렇게 안정감을 느낄 수 있는 장단조 으뜸화음을 구성해 주는 것이다.

'

장조와 단조에 익숙한 사람들에게는 이런 식의 음계가 혼란스럽기 그지 없는 괴악한 음계라는 생각이 들 법도 하다. 하지만 세상 모든 곡이 장단조로 구성되어 있다면 재미가 없지 않겠는가. 세상 모든 일이 이분법적으로 즐겁고 재미있는 일, 슬프고 어려운 일로만 구성되어 있는 것이 아니므로 즐겁지만 어려운 일도, 재미있지만 슬픈 일도 있는 것 아니겠는가. 장단조의 한계를 넘어서 제시되는 선법 기반의 음악 및 비(非)다이어토닉 음계(non-diatonic scale)는 청자들로 하여금 새로운 느낌을 주기에 충분하며 바로 이것을 지금 빈지노의 랩 음악에서조차 느낄 수 있는 것이다.

For the sake! Of the call!

-fluorF-