fluorF's Laboratory
웹사이트 소개
Introduction of the website
fluorF 소개
Introduction of fluorF
새로운 소식
News
하루 이야기
Daily essay
글
Articles
사진첩
Album
방명록
Guestbook
글
Articles
음악 5
Music 5
음악과 물리학
Music and Physics
피타고라스 음률
Pythagorean Tuning
지금까지 우리는 악기를 분류하고, 그 악기로부터 나오는 소리가 정상파에 의한 것임을, 그리고 피아노를 모델 악기로 삼아서 피아노의 현에 형성된 정상파가 어떻게 구성되어 있는지, 또 어떤 특징을 가지고 있는지 살펴 보았다. 이제는 화제를 조금 옮겨 '악기'보다는 '음' 자체에 조금 더 집중해보기로 한다. 그런데 왜 장의 제목이 피타고라스인가?

피타고라스는 매우 유명한 자연철학자이지만 수(數)를 신앙의 대상으로 삼은 종교 단체의 교주이기도 했다. 그래서 모든 것이 수로 이뤄져 있다고 믿은 피타고라스 (혹은 그의 학파)는 유리수로 표현되는 그 모든 조화에 대해 호기심을 갖고 연구를 진행했다. 그리고 그 연구 범위에는 음악도 있었다.

피타고라스 활동 당시 그리스 사람들은 하프와 같은 현악기에 대해 두 가지 사실을 경험적으로 알고 있었다.
- 현의 길이를 절반으로 줄여서 퉁기면 원래 현에서 나던 소리보다는 음높이가 높은데 아주 잘 어울리는 소리가 난다.
- 현의 길이를 2/3만 남기고 잘라낸 뒤 퉁기면 다른 소리가 나긴 하지만 역시 잘 어울리는 소리가 난다.
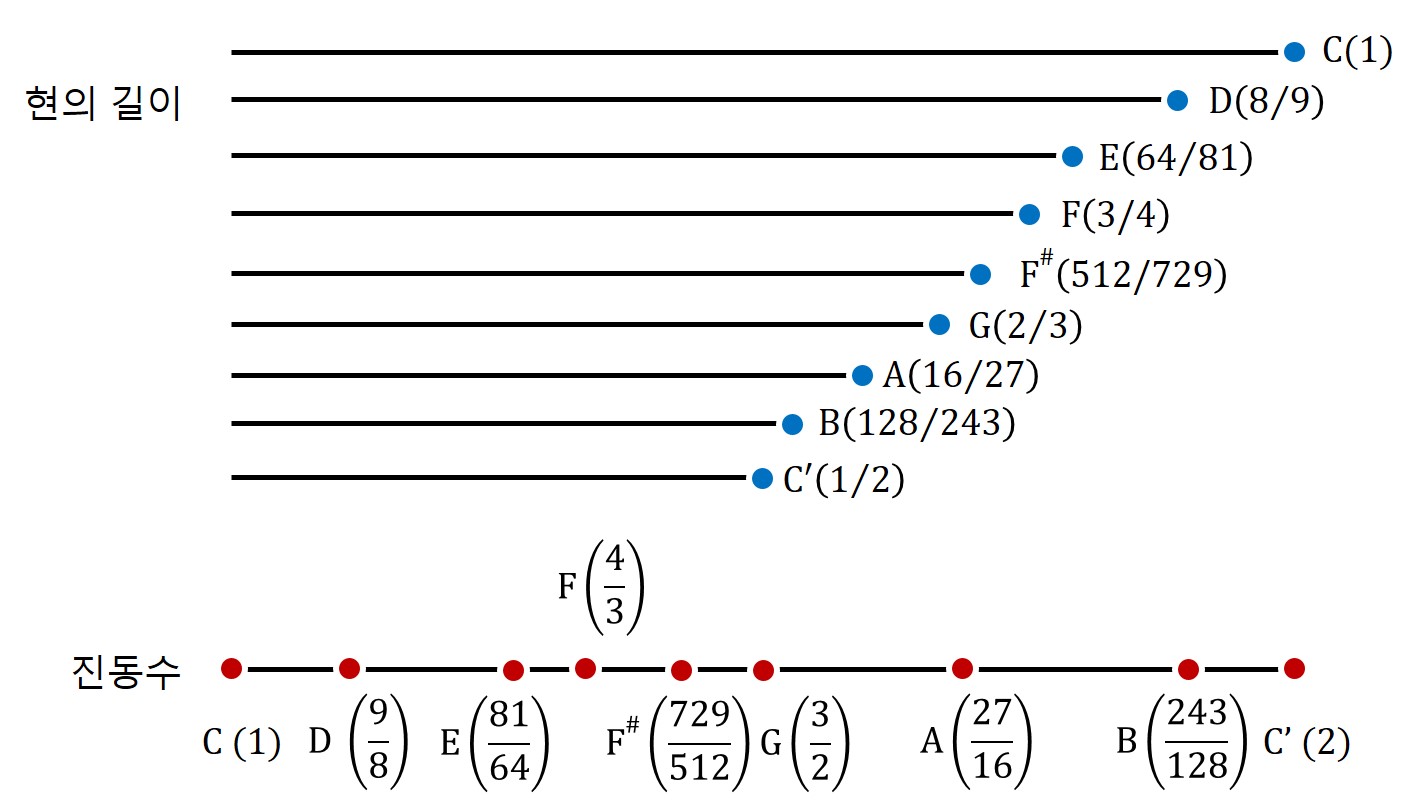
수에 관해 환장하던 피타고라스 학파는 여기서부터 다음 사실을 발견했다. 위의 사실로부터 현의 길이를 긴 것부터 차례대로 나열하면 1, 2/3, 1/2였다. 여기 사이에는 별 재미있는 사실을 발견하기 힘들다. 하지만, 역수를 취하면 어떻게 되는지 봤더니 1, 3/2, 2였다. 어라, 이것은 등차수열이다! 다시 말하지만 피타고라스 학파 사람들은 수를 신봉하는 사람들이었다. 역수를 취했더니 등차수열인 수열, 필자는 별로 그렇게 매력적이지 않게 들리는 성질이었지만 당시 피타고라스 사람들에게는 엄청난 대발견이었던 모양이다. 환호작약하던 그들은 이렇게 역수가 등차수열인 수열을 조화수열(調和數列, harmonic progression)이라고 불렀는데, 이는 현 길이의 관계가 음의 조화를 이룬다는 의미에서 비롯되었다고 한다.
그런데 정상파를 기억하고 있다면 조화수열에 대해 이렇게 이해할 수 있다. 동일한 물질로 구성된 현을 동일한 장력으로 매어두고 단지 길이만 달리한 뒤 퉁기는 것이기에 각 현에 생성된 정상파들의 속도(v)는 모두 동일하다. 하지만 기음의 정상파 형태를 생각해보면 알 수 있지만, 현이 짧아질수록 그 현에 생성되는 정상파의 파장(λ) 역시 짧아진다. 파동의 속도는 파장과 진동수의 곱이므로(v=fλ) 파장이 짧아질수록 진동수는 커지게 된다. 다시 말해 현의 길이만 조절하는 경우, 파장과 진동수는 반비례 관계에 있다. 그러므로 파장을 의미하는 현의 길이가 조화수열을 이룬다는 것은, 그것의 역수에 해당하는 진동수가 등차수열을 이룬다는 의미와 같다.
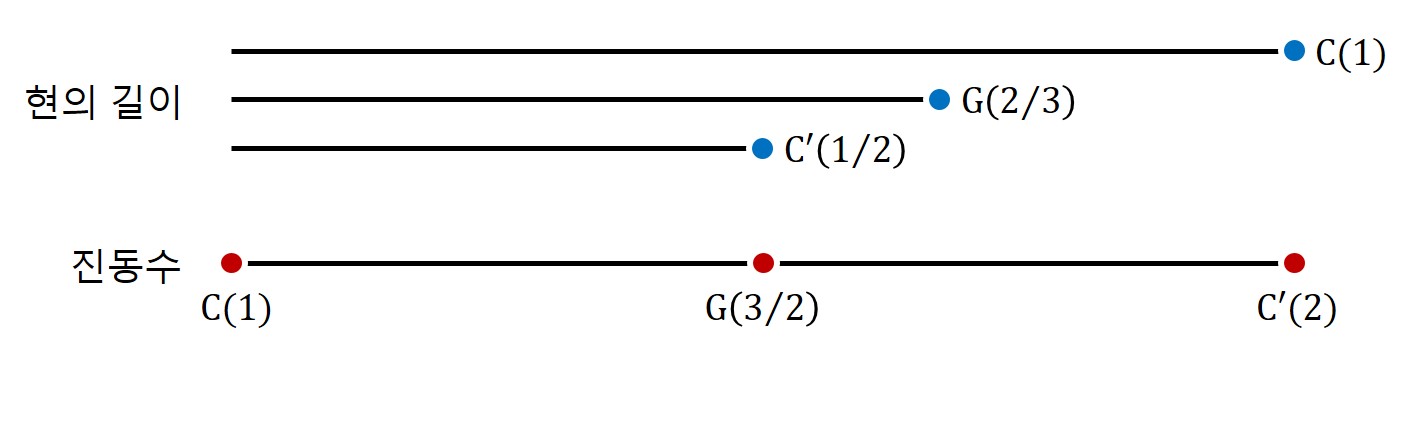
자, 그렇다면 C음을 가지고 이야기를 해보자. 이 C음과 가장 잘 어울리는 음은 무엇일까? 물론 자기 자신이다. 완벽하게 어울린다. 이 경우 현의 길이가 동일하므로 진동수의 비율은 1:1이 된다. 우리는 이것을 제주(齊奏, unison)라고 부른다.1
그 다음으로 잘 어울리는 음은? 현의 길이를 절반으로 해서 퉁긴 음이다. 이 음은 동일하게 C음이지만 음높이만 다른 음인데 파장의 비율이 1:2이므로 진동수의 비율은 거꾸로 2:1이 된다. 고대 그리스에서는 이 음정 간격을 디아파손(διαπασών)이라고 불렀는데, 우리 시대에는 이 두 음정의 간격을 옥타브(octave)라고 부르는데 이런 이름이 붙은 이유를 나중에 확인할 것이다. 편의상 이 음을 C'음이라고 쓰겠다.
그 다음으로 잘 어울리는 음은? 현의 길이를 2/3으로 해서 퉁긴 음이다. 파장의 비율이 2:3이므로 이 음과 C음의 진동수 비율은 3:2가 된다. 고대 그리스에서는 이 음정 간격을 디아펜테(διαπέντε)라고 불렀다고 하는데 우리 시대에는 이 두 음정의 간격을 완전 5도(perfect fifth)라고 부른다. 그리고 이 음은 이 경우 G음에 해당한다.

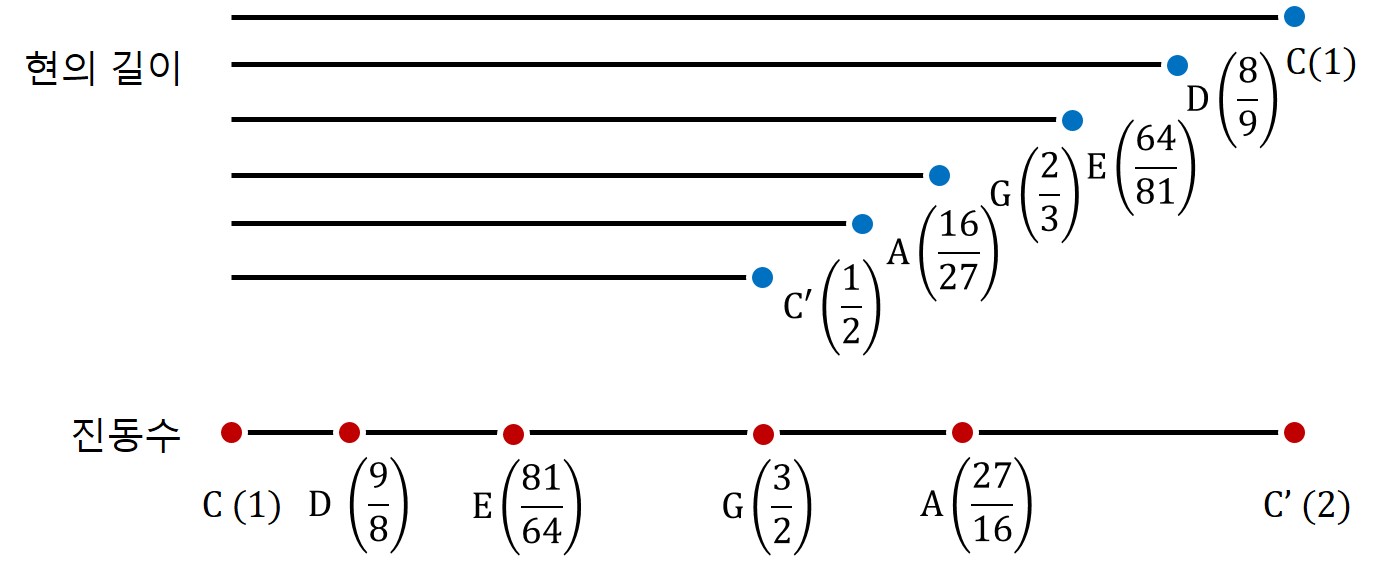
아무튼 경험적으로 우리는 C음과 G음을 찾았다. 음 높이 순서는 C, G, 그리고 C'. 따라서 C, G 두 음만 사용하면 굉장히 안정적이고 조화로운 음악을 만들 수 있다. 그런데 그렇게 두 음만 사용하면 너무 단순하잖아? 세상에 음이 두 개만 있는 것은 아니지 않은가. 사실 세상에 적어도 두 개보다는 더 많은 음이 있다는 것은 누구나가 다 아는 이치였다. 아무리 수천년 전 사람이더라도 현악기를 다루는 사람이라면 손을 어디에 짚느냐에 따라 무수하게 다양한 음이 발생하는 것을 경험적으로 다들 알고 있었다. 즉 다시 말하면, 모두들 C음과 C'음 사이에는 무수하게 많은 음들이 계단처럼 존재할 것이라는 것을 알고는 있었다.
하지만 피타고라스 학파의 생각은 경험을 넘어선 수 중심의 사고였다. 이들은 C음과 C'음 사이에 아무렇게나 음의 계단을 놓는 것을 배격했다. 그럼 어떻게? 앞서 살펴본 조화수열을 활용하는 것이었다. 즉 앞서 살펴본 진동수의 유리수 비율, 곧 2:1과 3:2의 관계를 활용해서 사이에 있는 음들을 찾아내자는 것이다. 그렇게 되면 C음과 C'음 사이에는 모두 조화수열의 관계로 구성된, 곧 수학적으로 매우 아름다운 유리수 비율로 정의된 음의 계단이 놓일 것이다. 이 얼마나 조화로운지!
이제 그 음계(音階, scale)를 찾아나서는 여정을 떠날 것이다.
음계를 찾는 여정을 떠나기 전에 일단 우리가 알고 있는 사실을 표시하면 아래와 같다.
자, C로부터 G가 나왔으니 이제 G음과 잘 어울리는 음을 찾아보자. 다음과 같은 방식으로.
- 길이가 2/3인 현을 반으로 자르면 G'음인데 이건 똑같은 G음이니까 다른 음을 찾기 위해 진동수 비율 3:2를 이용해 보자.
- 그러려면, 현의 길이를 또 2/3 으로 잘라서 퉁겨 봐야지.
- 어라? 그랬더니 현의 길이가 4/9가 되어서 C’ 보다 더 짧잖아.
- C와 C' 사이에 들어와야 하니까 한 옥타브 낮추면 되겠지. 그러니 줄 길이를 두 배로 하자
- 그래서 현의 길이는 8/9가 되었다. 이건 D음!
따라서 G음으로부터 우리는 현의 길이가 8/9인 D음을 얻었다.
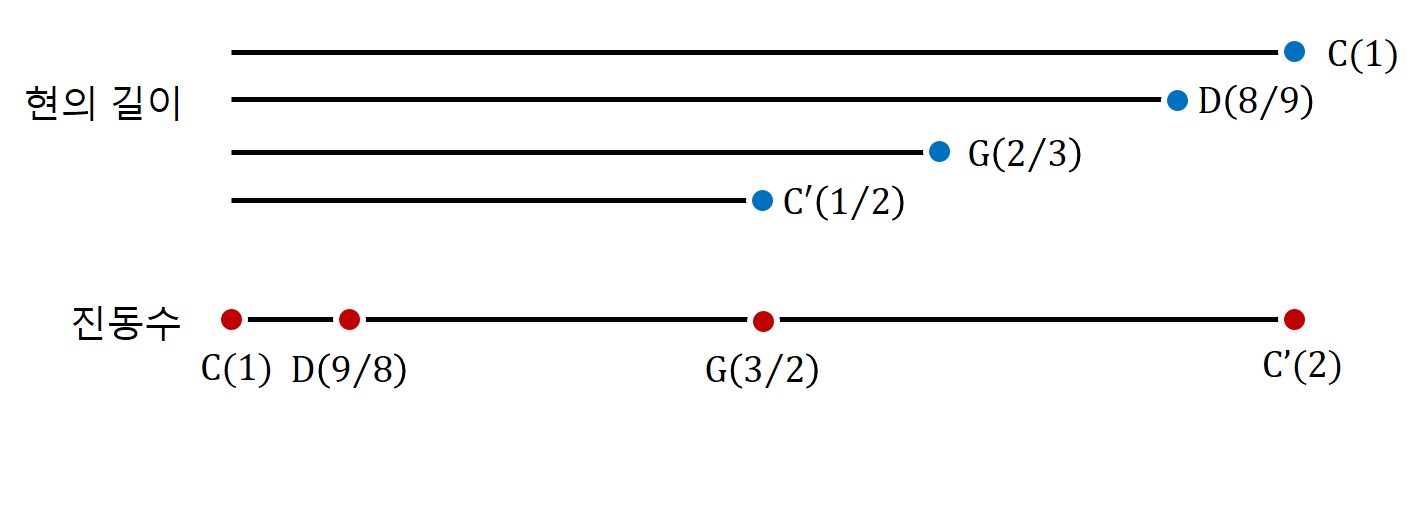
D음으로부터 조화로운 음을 찾는 여정은 계속된다.
- 이번에도 진동수 비율 3:2를 이용하자.
- 그러려면, 현의 길이를 또 2/3 으로 잘라서 퉁겨 봐야지.
- 어라? 그랬더니 현의 길이가 16/27가 되는군. 이건 A음!
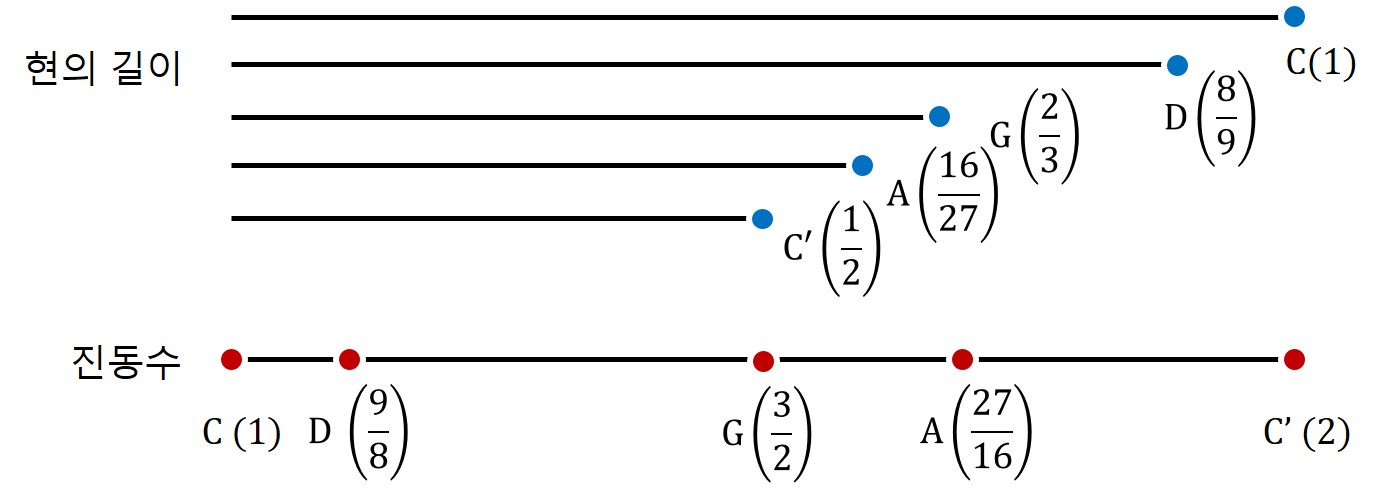
여정은 계속된다. 이제는 A음에서 시작해 보자.
- 이번에도 진동수 비율 3:2를 이용하자.
- 그러려면, 현의 길이를 또 2/3 으로 잘라야지. 어라? 현의 길이가 32/81 가 되어서 C’ 보다 더 짧잖아. 그럼 한 옥타브 낮춰야 하니까 현의 길이를 2배로 늘려줘야겠네.
- 그래서 현의 길이는 64/81가 되었다. 이건 E음!
이와 같은 과정을 피타고라스 음률(Pythagorean tuning)이라고 부른다. 그런데 이 과정을 사실 산수 측면에서 살펴보면 다음 문제와 같다.
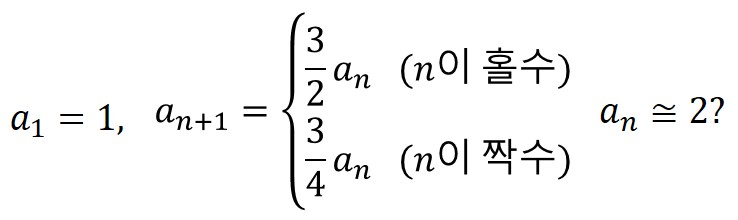
여기서 수열 an는 현의 진동수를 의미한다. 우리의 목적은 한 옥타브 위의 음(=2)이 나올 때까지 수열을 구하는 것이니, 결국 피타고라스 음률을 이용한 음계 찾기 놀이는 위의 법칙에 따라 수열을 구하는 도중에 2를 발견할 때 '그만!'을 외치는 게임이나 다름없다.
| an | 값 | 2에 대한 비율 |
|---|---|---|
| a1 | 1 | 50% |
| a2 | 1.5 | 75% |
| a3 | 1.125 | 56% |
| a4 | 1.6875 | 84% |
| a5 | 1.265625 | 63% |
| a6 | 1.8984375 | 95% |
오, a6는 2에 95% 가까우므로 여기서 스톱을 외쳐도 될 것 같다. 그 말은 음을 5개 찾고 나서 진동수 3:2 비율을 이용하여 다음 음을 찾으면 C'음이라고 볼 수 있다는 말이니 C음과 C'음 사이에 5개의 계단이 있다는 뜻이다. 가만, 우리가 지금까지 어떤 음을 찾았더라? C, D, E, G, A, C' 였다. 우리는 이렇게 구성된 음계를 펜타토닉 스케일(pentatonic scale)이라고 한다. 참고로 앞으로 음계를 언급할 때 앞의 단어가 영어이면 스케일이라고 표현하고 한국어이면 음계라고 표현할 것이다. 즉, 5음계이지만 5스케일이 아니며 펜타토닉 스케일이지만 펜타토닉 음계는 아니다.
그리스어의 접두어 펜타(πεντα-, penta-)는 5를 뜻한다.2 이 펜타토닉 스케일은 우리에게 굉장히 익숙하다. 아래 음악을 들어보면 펜타토닉 스케일이 어떤 것인지 대번에 알 수 있을 것이다.
굉장히 민요스러운 음계 아닌가. 그래서 5음계는 세계 각지의 민요에서 많이 찾아볼 수 있다. 그런데 이 펜타토닉 스케일이라는 단어는 실용음악 연주자들에게도 꽤나 익숙한 단어로, 솔로 연주나 즉흥 연주할 때 펜타토닉 스케일이 굉장히 많이 쓰인다. 위대한 색소포니스트인 재즈 연주자 존 콜트레인(John Coltrane)의 명반(名盤) 중 하나로 꼽히는 「Giant Steps」의 색소폰 즉흥 연주 파트에는 펜타토닉 스케일이 빈번하게 쓰인다.
그런데 C, D, E, G, A 의 음을 찾기는 했는데 무조건 음계가 C 부터 시작할 필요는 없지 않을까? 순서는 그대로 둔채 시작음만 달리하면 어떨까? 예를 들면 구성음은 그대로 두고 A부터 시작하는 음계를 만들면 다음과 같을 것이다: A, C, D, E, G, A'.

이렇게 형성된 음계는 우리나라 전통 민요에서도 찾아볼 수 있으니 그것이 바로 계면조(界面調)이다. 마이너 펜타토닉 스케일의 대표적인 곡은 바로 「밀양 아리랑」이다.
서양 음악 이야기만 줄창 하다가 국악이 나오니 희한하다 싶겠지만, 사실 피타고라스 음계 찾기 놀이는 그리스 사람들만 한 게 아니라 중국 사람들도 고대 시기에 이미 진행한 바 있다. 사람들의 경험이나 생각은 동서고금을 막론하고 다 똑같기 마련이니. 그래서 동아시아에서도 피타고라스 음계와 매우 유사한 5음계가 성립되었는데 소위 '궁(宮), 상(商), 각(角), 치(徵), 우(羽)'가 바로 그것이다. 아무튼 국악 이야기가 나왔으니 내친 김에 하나 더 알아보고 가자. 만일 펜타토닉 스케일이 G부터 시작하면 G, A, C, D, E, G'의 음계가 만들어질 것이다. 그리고 이것은 평조(平調)이다. 이런 스케일의 대표적인 곡은 바로 「경기 아리랑」이다.
피타고라스 음계 찾기 놀이 도중 6번째 수열 원소를 찾았을 때 우리는 2에 95% 가까운 수준에서 만족했고, 그 결과 나온 것이 펜타토닉 스케일이었다. 그런데 이 5%의 차이에서 그대로 놀이를 끝낼 것인가? 혹시 조금만 음을 더 찾다보면 2에 더 가까운 숫자가 나올 수 있지 않을까? 이제 펜타토닉 스케일을 뒤로한 채 피타고라스 음률을 조금 더 진행해 보자. E음에서 끝났었지 아마?

자, E음과 어울리는 음을 아까와 같은 방식으로 찾아보자.
- 이번에도 진동수 비율 3:2를 이용하자.
- 그러려면, 현의 길이를 또 2/3 으로 잘라야지.
- 그래서 현의 길이는 128/243가 되었다. 이건 B음!
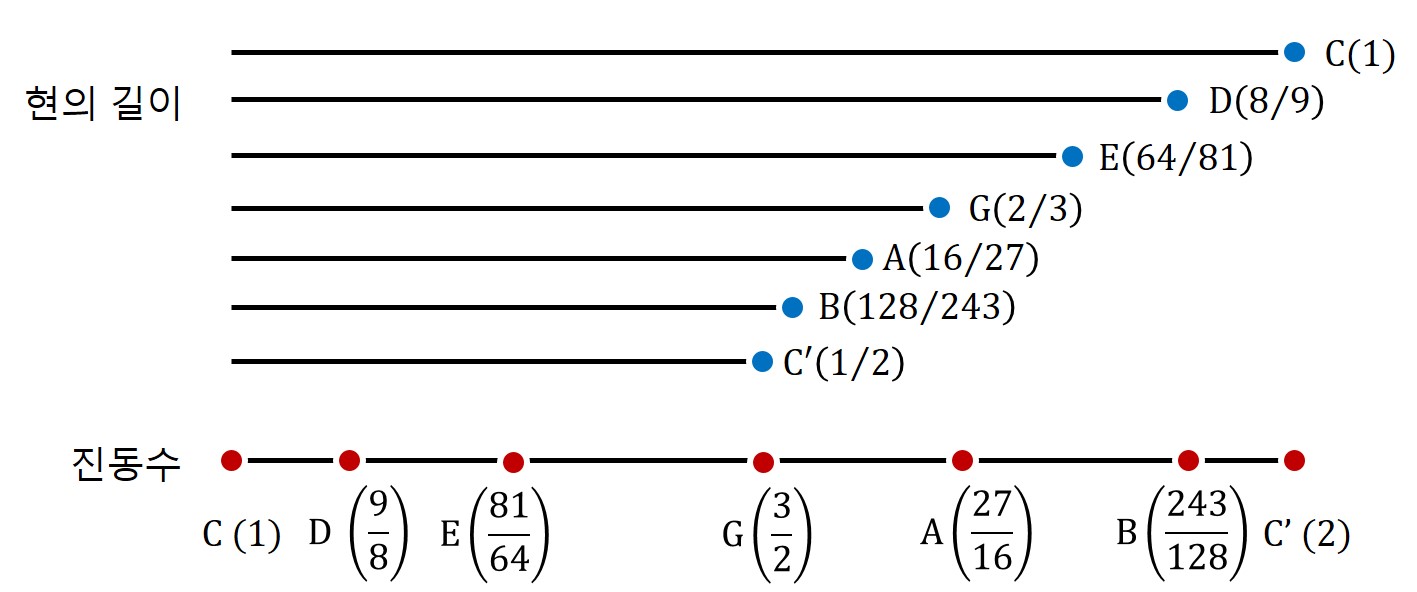
이번에는 B음과 어울리는 음을 또 찾아보자.
- 이번에도 진동수 비율 3:2를 이용하자.
- 그러려면, 현의 길이를 또 2/3 으로 잘라야지. 어라? 현의 길이가 256/729 가 되어서 C’ 보다 더 짧잖아. 그럼 한 옥타브 낮춰야 하니까 현의 길이를 2배로 늘려줘야겠네.
- 그래서 현의 길이는 512/729가 되었다. 이건 F#음!
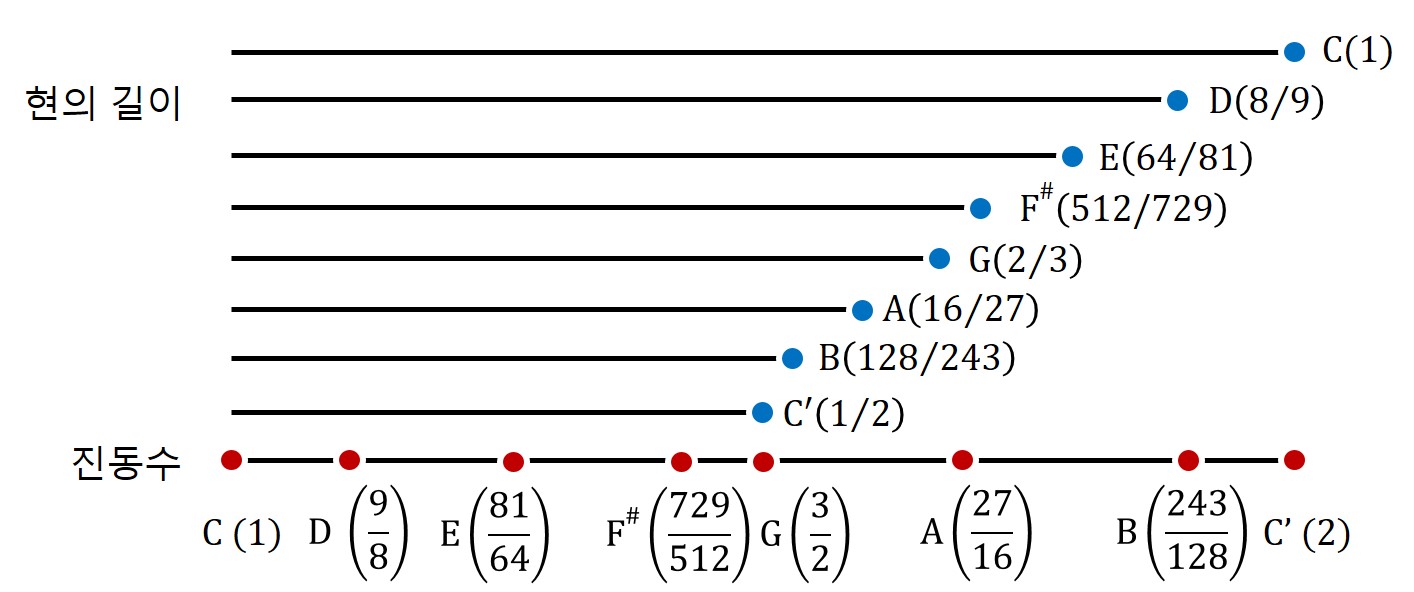
총 7음을 찾았는데 아까처럼 수열을 표로 그려보면 다음과 같다.
| an | 값 | 2에 대한 비율 |
|---|---|---|
| a1 | 1 | 50% |
| a2 | 1.5 | 75% |
| a3 | 1.125 | 56% |
| a4 | 1.6875 | 84% |
| a5 | 1.265625 | 63% |
| a6 | 1.8984375 | 95% |
| a7 | 1.423828125 | 71% |
| a8 | 2.1357421875 | 107% |
8번째 원소가 107%이므로 굉장히 2에 가깝다고 할 수 있겠다. 그러므로 여기서 스톱을 외쳐도 될 것 같다. 다시 부연 설명하자면, 이 말은 음을 7개 찾고 나서 진동수 3:2 비율을 이용하여 다음 음을 찾으면 C'음이라고 볼 수 있다는 말이니 C음과 C'음 사이에 7개의 계단이 있다는 뜻이다. 가만, 우리가 지금까지 어떤 음을 찾았더라? C, D, E, F# G, A, B, C' 였다.
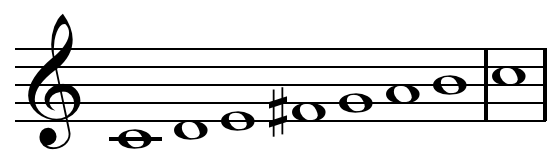
따라서 우리는 7음계를 찾았으므로 펜타토닉 스케일의 예를 따라 이를 헵타토닉 스케일(heptatonic scale)이라고 부를 수도 있겠지만, 전통적으로 이렇게 찾은 음계를 특별히 다이어토닉 스케일(diatonic scale)이라고 하며 우리말로는 온음계라고 한다. 그리스어 접두어 디아(δια-, dia-)는 '~을 통해'라는 뜻을 담고 있으므로 다이어토닉 스케일이란 음정을 통해 진행하는 스케일, 뭐 이런 정도로 해석할 수 있겠다.3 이 음계에 따르면 C에서 C'까지 음이 7개 있으므로 C'는 C 입장에서 8번째 음이 된다. 그런 이유로 C와 C' 음정 간격을 라틴어로 '8번째'를 의미하는 'octavus'에서 따와 옥타브라는 이름이 붙은 것이다.
그런데 이 음계를 구성한 음정간의 간격을 자세히 살펴보면 흥미로운 점을 발견할 수 있다. 음정간의 간격을 진동수 비율로 표현하면 딱 두 종류인데, 하나는 9/8, 다른 하나는 256/243이다. 흥미롭게도 9/8에 제곱근을 씌우면 값이 대략 1.061인데, 이 값은 256/243(=1.053)과 매우 비슷한 값이다. 이런 이유로 9/8 비율은 다이어토닉 스케일에서 음정 간격의 기준으로 인식되었는데 피타고라스는 이를 에포그도온(επογδοον)이라고 불렀고,4 현재 우리는 이것을 온음(whole tone)이라고 부른다. 한편 256/245이란 값은 일종의 기하평균(geometric mean)값인데 우리는 현재 이 음정 간격을 반음(half tone 혹은 semitone)이라고 부른다.
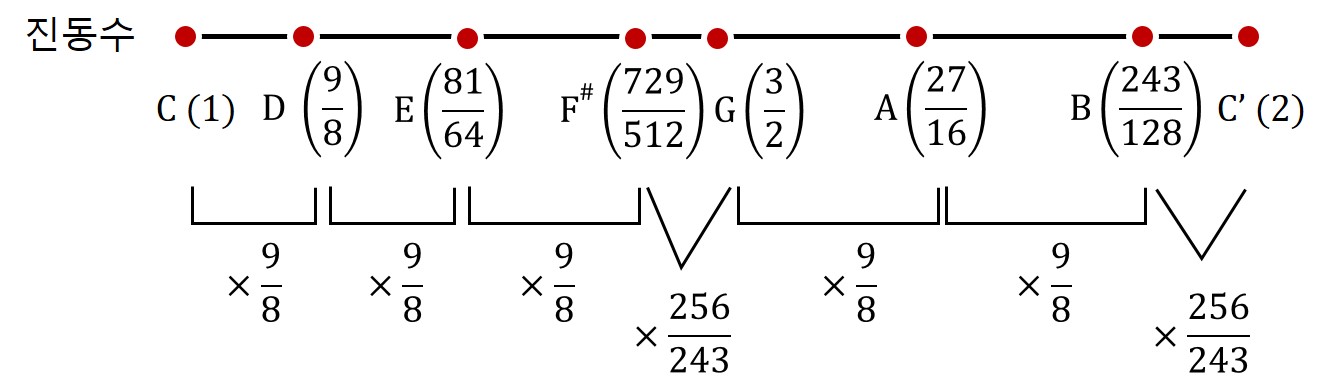
한 옥타브 사이에서 아무렇게나 일곱 음을 대충 골라 뽑으면 그게 곧 헵타토닉 스케일이지만, 다이어토닉 스케일이 잡다한 다른 헵타토닉 스케일과 비교되는 점이 여기에 있다. 바로 한 옥타브가 5개의 온음, 그리고 2개의 반음으로 구성되어 있다는 점이다. 괜히 어린 나이에 허구한날 온음, 온음, 반음, 온음 이런 걸 외우는 게 아니다. 그만큼 상당히 중요한 음계 이론의 하나이므로 온음과 반음 음정 간격에 대한 지식을 어렸을 때부터 완전히 체화시키는 것이 중요하다. 물론 당시에는 흰 건반 사이에 검은 건반이 있으면 온음, 검은 건반이 없이 흰 건반이 나란히 있으면 반음, 이런 식으로 외웠지만 배경에는 이와 같은 진동수 비율의 조화가 숨어 있었던 것이다.
앞서 펜타토닉 스케일의 시작음을 달리함으로써 마이너 펜타토닉 스케일이라든지 평조라든지 다양한 음계를 만들어낼 수 있었는데, 마찬가지로 지금 위에서 구성한 다이어토닉 스케일 역시 시작음을 달리함으로써 다른 느낌을 주는 다양한 음계를 만들어낼 수 있을 것이다. 우선 앞에서 언급한 C, D, E, F#, G, A, B, C' 는 음정간격이 온음-온음-온음-반음-온음-온음-반음 ㅡ 앞으로 표기의 편리성을 위해 온음을 W, 반음을 H라고 쓰고 WWWHWWH로 쓰겠다. ㅡ 이므로 4-5음과 7-8음이 반음이다. 이런 식으로 구성된 다이어토닉 스케일을 리디안 선법(旋法), 혹은 리디안 모드(Lydian mode)라고 한다.5 C음부터 시작하니까 C 리디안 모드가 되겠다.

D부터 시작하면 음계는 D, E, F#, G, A, B, C', D'가 될 것이다. 음정 간격이 WWHWWHW 이므로 3-4음과 6-7음이 반음이다. 이와 같은 다이어토닉 스케일을 믹솔리디안 모드(Mixolydian mode)라고 한다. D음부터 시작하니까 D 믹솔리디안 모드가 되겠다.
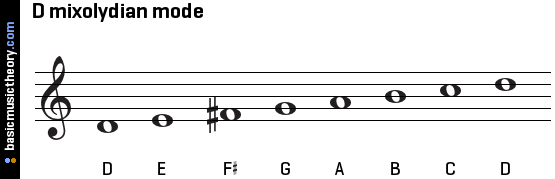
E부터 시작하면 음계는 E, F#, G, A, B, C', D', E'가 될 것이다. 음정 간격이 WHWWHWW 이므로 2-3음과 5-6음이 반음이다. 이와 같은 다이어토닉 스케일을 에이올리안 모드(Aeolian mode)라고 한다. 그런데 2-3음과 5-6음이 반음인 음계를 우린 학교 음악 시간에 배운 적이 있었다. 바로 이 모드는 훗날 확립된 자연 단음계(natural minor scale)와 동일한 음계라고 볼 수 있다.
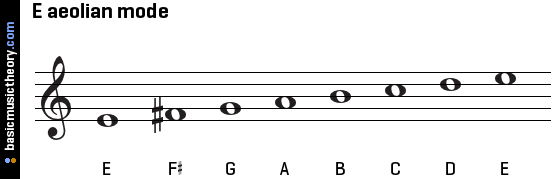
F#부터 시작하면 음정 간격이 HWWHWWW 이므로 1-2음과 4-5음이 반음이다. 이와 같은 다이어토닉 스케일을 로크리안 모드(Locrian mode)라고 한다.
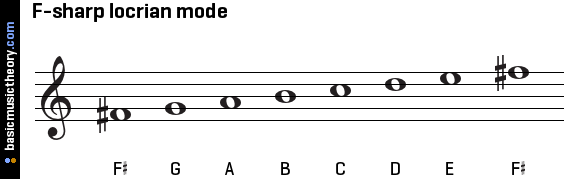
G부터 시작하면 음정 간격이 WWHWWWH 이므로 3-4음과 7-8음이 반음이다. 이와 같은 다이어토닉 스케일을 아이오니안 모드(Ionian mode)라고 한다. 어라? 이것도 우리 배운 바 있다. 바로 이 모드는 훗날 확립된 장음계(major scale)와 동일한 음계라고 볼 수 있다.

A부터 시작하면 음정 간격이 WHWWWHW 이므로 2-3음과 6-7음이 반음이다. 이와 같은 다이어토닉 스케일을 도리안 모드(Dorian mode)라고 한다.

마지막으로, B부터 시작하면 음정 간격이 HWWWHWW 이므로 1-2음과 5-6음이 반음이다. 이와 같은 다이어토닉 스케일을 프리지안 모드(Phyrigian mode)라고 한다.

우리는 장음계, 단음계가 어떤 지배적인 중심 음계로 자리 잡은 시대에 살고 있으므로 기준을 아이오니안 모드, 그것도 가장 간단하다고 인식되는 C 아이오니안 모드에 맞추면 이해가 상당히 쉬워진다. 만약 우리가 피타고라스 음계 찾기 놀이를 C음부터 진행하지 않고 F음부터 진행했다면, C 아이오니안 모드를 찾을 수 있는데 그것은 현대 C 장음계와 동일한 C, D, E, F, G, A, B, C'음들로 구성된 음계로, 피아노에서 이것을 연주하려면 가온다에서부터 흰 건반만 연주하면 된다.
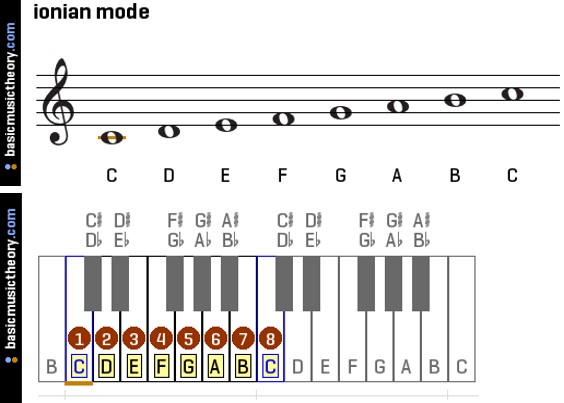
그리고 여기서부터 얻어지는 모드를 나열하면 아래 표와 같다.
| 모드 | 구성음 | 반음 위치 | 다른 이름 |
|---|---|---|---|
| C 아이오니안 모드 | CDEFGABC | 3-4 / 7-8 | 장음계 |
| D 도리안 모드 | DEFGABCD | 2-3 / 6-7 | |
| E 프리지안 모드 | EFGABCDE | 1-2 / 5-6 | |
| F 리디안 모드 | FGABCDEF | 4-5 / 7-8 | |
| G 믹솔리디안 모드 | GABCDEFG | 3-4 / 6-7 | |
| A 에이올리안 모드 | ABCDEFGA | 2-3 / 5-6 | 자연 단음계 |
| B 로크리안 모드 | BCDEFGAB | 1-2 / 4-5 |
이 선법들은 중세 시대까지 교회에서 교회 음악을 연주할 때 많이 쓰였는데, 장음계와 단음계가 확립되기 이전까지 서양 음악의 주류였다. 그러다가 르네상스 시기 이후 선법의 사용은 점차 줄어들었지만 오히려 현대에 들어와서 선법 음계가 주는 독특한 느낌이 재조명받게 되었다. 재즈 및 현대 음악사에서 절대 빼놓을 수 없는 전설적인 선법 음악들이 여럿 있는데 그 중 하나가 저 유명한 모달 재즈(modal jazz)의 신호탄으로 여겨진 앨범 『Kind of a Blue』의 1번 수록곡「So What」이다. 이 곡은 D 도리안 모드를 중심 음계로 사용하고 있으며 장음계와 단음계와는 구별되는 굉장히 독특한 느낌을 선사한다.
그리고 필자가 생각해봤는데, 악명 높은 피아노 연습곡의 대명사인 아농(Hanon)의 연습곡들은 비록 의도하지는 않았어도 같은 음렬을 일곱가지 선법에서 색다르게 모두 경험할 수 있다.
하지만 음계를 찾는 여정은 아직 끝나지 않았다.
우리가 C로부터 F#까지 찾아 나가는 방법은 진동수 비율 3:2를 이용해서 먼저 현의 길이를 2/3 자르고 두 배로 늘리던가 했던 방식이었다. 그런데 F#의 진동수 비율이 512/729로 분수 숫자가 너무 커져서 복잡해질 것이 뻔하므로 이번에는 다른 방법을 사용해보자. 거꾸로 해 보는 것이다. 즉, 진동수 비율을 2:3으로 해서 C음 현의 길이를 3/2배로 늘린다음 절반으로 자르든지 하는 것이다.
- 진동수 비율 2:3을 이용하자.
- 그러려면, 현의 길이를 3/2 으로 늘려줘야지. 당연히 C보다 더 길어질테니 한 옥타브 높여야 하니까 현의 길이를 1/2로 잘라 줘야겠네.
- 그래서 현의 길이는 3/4가 되었다. 이건 F음!
이후로 계속 이 과정을 진행해야 하는데, 이 반복적인 과정을 또 보여주면 페이지 길이만 늘어나고 재미가 없을 것이다. 그러니 먼저 앞에서 진행했던 수열 찾기 놀이를 먼저 한 다음에 한꺼번에 이를 보여주도록 하겠다. a8까지는 앞에서 나타냈으니, a9부터 시작하겠다.
| an | 값 | 2에 대한 비율 |
|---|---|---|
| a9 | 1.601806640625 | 80% |
| a10 | 2.4027099609375 | 120% |
| a11 | 1.80203247070312 | 90% |
| a12 | 2.70304870605468 | 135% |
| a13 | 2.02728652954101 | 101% |
뭐? 101%? 지금까지 있었던 숫자보다 2에 가장 초근접한 숫자가 나타났다! 13번째 원소이므로 이 말은 즉 한 옥타브가 12음정으로 구성되어 있다는 뜻이다. 그리고 그것을 그림으로 나타내면 다음과 같다.
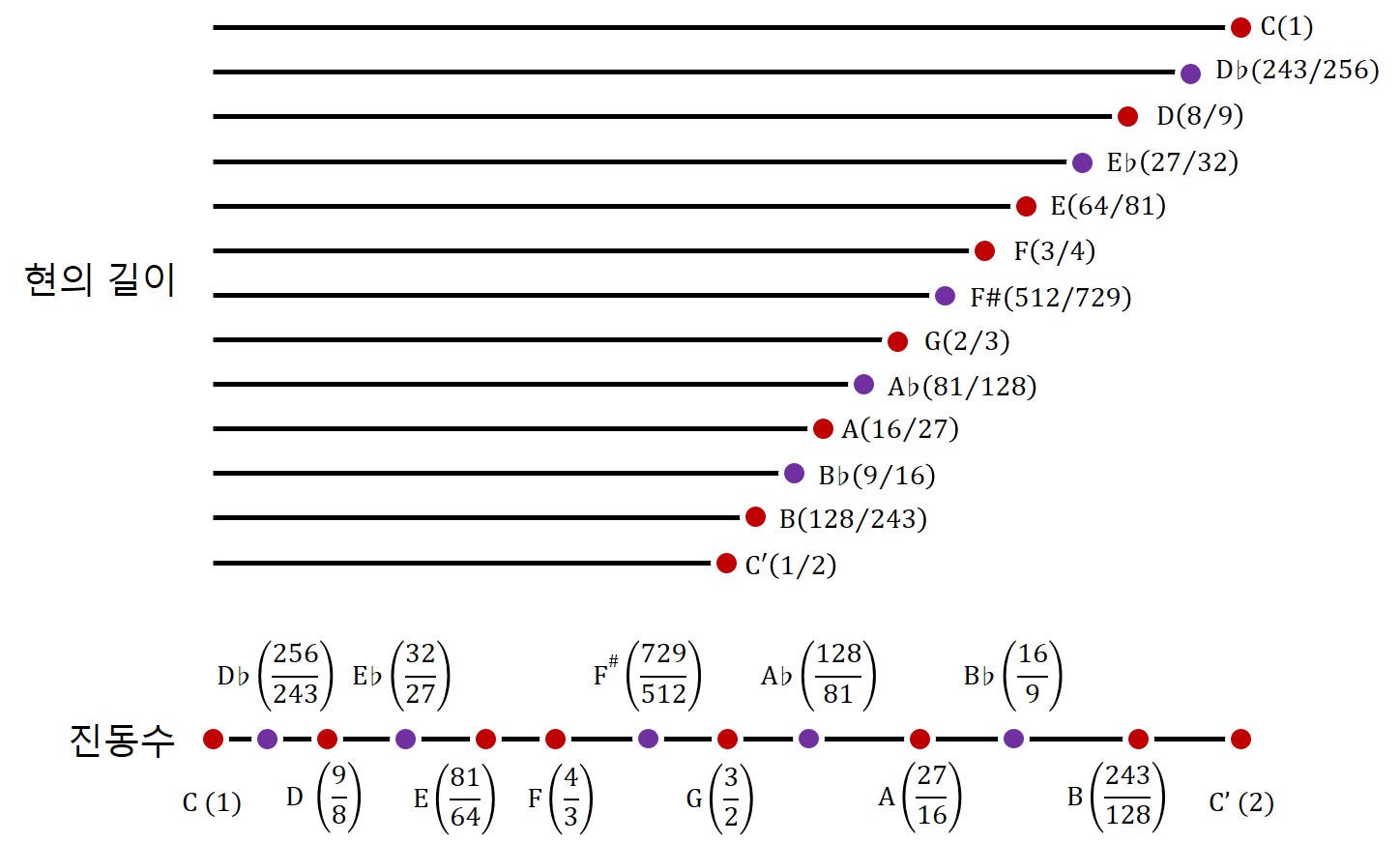
이와 같은 12음계는 도데카토닉 스케일(dodecatonic scale)이라고 부를 수 있지만, 역시 고대 그리스 음악학의 전통에 따라 이렇게 찾은 음계를 특별히 크로매틱 스케일(chromatic scale)이라고 하며 우리말로는 반음계라고 한다. 그리스어 접두어 크로모(χρωμο-, chromo-)는 '색깔'이라는 뜻을 담고 있는데 다이어토닉 스케일에서 벗어난 음정 간격을 통해 색다른 느낌을 선사하는 스케일, 뭐 이런 정도로 해석할 수 있겠다.6

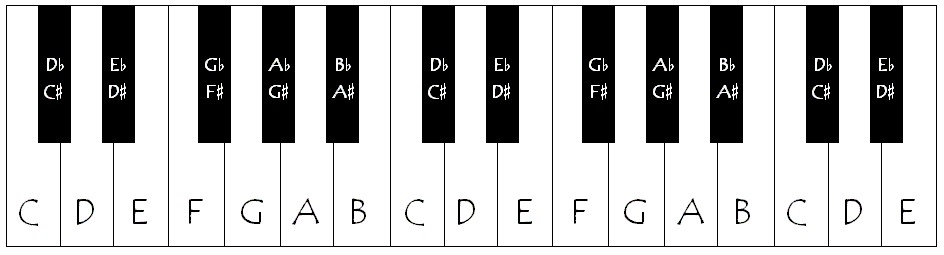
한 옥타브의 음정 간격 사이에 성립된 다이어토닉 스케일은 7음, 크로매틱 스케일은 12음으로 구성되었다는 사실을 알게 되는 순간부터 피아노 건반이 왜 아래 그림처럼 생겼는지 그 힌트를 얻을 수 있다. 처음에 피아노를 배울 때에는 그냥 무조건적으로 저것은 C, 저것은 F, 저것은 A#이니라... 뭐 이런 식으로 외웠지만 말이다.
3편의 피아노 발전사에서 언급했지만, 서양 음악사에 등장하는 최초의 건반 악기는 오르간이라고 했다. 그리고 그 오르간은 대체로 교회 음악을 연주하는데 사용되었다. 따라서 오르간의 건반 배치는 교회 음악 연주에 적합한 형태여야 했는데, 서양 교회 음악의 주류는 교황 그레고리오 1세에 의해 확립되었다고 하는 교회 선법(혹은 그레고리안 선법, Gregorian mode)이었다. 이것은 고대 동방 정교회에서 활용되었던 고대 시기의 옥토에코스(οκτωηχος)의 영향을 받았던 것으로 알려져 있는데, 서양 교회의 선법은 동방 교회의 선법과는 달랐지만 이 옥토에코스에서 사용하던 명칭(도리안, 하이포도리안, 프리지안, 하이포프리지안, 리디안, 하이포리디안, 믹솔리디안, 하이포믹솔리디안)을 차용하여 4개의 정격 선법과 4개의 변격 선법으로 구성된 8개의 선법을 확립하였다.

B음의 경우 때에 따라 반음 내린 B♭음을 대신 사용하였다.
위 그림에서 알 수 있듯이 교회 선법에서 주로 사용되는 음은 8음이었는데 B, C, D, E, F, G, A, B♭였다.7 한 옥타브에 음이 12개가 있는데 8개가 주로 쓰였으니 자연스럽게 4개의 음은 적어도 교회 음악에서는 부속음 취급을 받은 것이다. 따라서 초기 교회 오르간 건반은 8개의 건반을 기본으로 한 4개의 부속 건반이 두개씩 대칭적으로 중간에 껴들어 간 형태였다. B, C, "C#," D, "D#," E / F, "F#," G, "G#," A, B♭ 이런 식으로.
그러다가 중세 시대를 거치면서 교회 선법이 점차 약화되면서 B♭가 누리던 특수한 지위는 몰수되었고, 다이어토닉 스케일을 구성하는 7음(C, D, E, F, G, A, B)만이 흰 건반으로 남는 방향으로 수정이 이뤄지게 되었다. 그 결과 12음 중 나머지 5음은 부속음으로서 7음을 표현하는 흰 건반 사이 사이에 검은 건반으로서 껴들어가 위 그림과 같은 지금의 건반 형태가 나타난 것이다. 즉, 피아노의 흰 건반은 선법의 영향으로 인해 다이어토닉 스케일을 표현하는 음들로 구성이 된 것이고 검은 건반은 크로매틱 스케일에서 다이어토닉 스케일을 뺀 나머지 음들로 구성된 것이다.
재미있는 것은 검은 건반만 순서대로 치면 이것은 처음에서 언급했던 진동수 비율을 가진 펜타토닉 스케일이 된다. 크로마토 스케일이 12음이고 다이어토닉 스케일이 7음인데 그 12음에서 7음을 뺀 5음이 펜타토닉 스케일을 구성한다는 것이다. 혹시 어린 아이들이 피아노를 가지고 놀 때 검은 건반만으로 장난치며 음을 마구 눌러대도 왠지 이상하게 그럴 듯하게 들린다는 생각을 혹시 해 본 적이 없는가? 거기에는 다 이유가 있었던 것이다. 아이들은 완전 5도와 옥타브로 구성된 펜타토닉 스케일의 음을 눌러댔기 때문에 우리 귀에 부조화스럽게 들리지 않았던 것이다. 심지어 프레데릭 쇼팽(Frédéric Chopin)은 검은 건반으로 구성된 연습곡(Étude)을 작곡하기도 했다.8
반음계의 사용이 굉장히 잘 드러나는 곡 중 하나가 바로 클로드 드뷔시(Claude Debussy)의 목신의 오후 전주곡(Prélude à l'après-midi d'un faune)이다. 플룻의 첫 테마 연주와 하프의 연주를 들어보면 알 수 있다.
이제 우리의 피타고라스 음계 찾기 놀이는 어느 정도 끝난 듯 하지만 욕심이 있는 사람들은 12음에서 멈추지 않고 수열 찾기를 더 진행할 것이다. 실제로 그런 과정을 반복하면 다음과 같은 사실들을 알 수 있다.
- a18은 3.848677..이 되는데, 이 값은 2가 아닌 4에 96% 가까운 값이다. 두 옥타브가 17음으로 구성되어 있다면 한 옥타브도 비례하여 17음으로 나눌 수 있다는 뜻이다. 여기서부터는 반음보다도 더 음정 간격이 작은 미분음(microtone)들이 등장하게 된다.
- a20은 4.329761..이 되는데, 이 값은 역시 4에 대해 108%인 값이다. 즉, 한 옥타브를 19음으로 나눌 수 있다는 뜻이다. 생각보다 이 19음계는 역사가 오래되었는데 16세기에 이미 제안된 바 있다고 한다.
- a25은 4.109891..이 되는데, 이 값은 4에 대해 102%인 값이다. 즉, 한 옥타브를 24음으로 나눌 수 있다는 뜻이다. 24음계는 12음계의 정확히 두 배이므로 각 음정간의 간격이 반음이 아니라 반의 반음, 즉 사분음(四分音, quarter tone)이 된다. 관악기들은 이 사분음을 표현할 수 있기 때문에 24음계 역시 특수하게 고려될 수 있는 음계가 된다.
- a32은 8.777667..이 되는데, 이 값은 8에 대해 110%인 값이다. 즉, 한 옥타브를 31음으로 나눌 수 있다는 뜻이다. 31음계는 네덜란드의 물리학자인 크리스티안 하위헌스(Christian Huygens)도 제안한 적이 있다고 한다.
이렇게 하다가는 한도 끝도 없을테니 이쯤에서 그만 두어야 할 것 같다. 아무튼 한 옥타브 음정 간격 하에서 음계를 찾는 여정은 피타고라스 학파의 기여를 통해 진행될 수 있었고, 우리는 그 여정 가운데 펜타토닉 스케일, 다이어토닉 스케일, 크로매틱 스케일을 찾아낼 수 있었다.
그러나 여기서 완벽히 문제가 끝났으면 좋으련만. 아주 큰 문제가 발생하고 만다.
우리가 최종적으로 얻었던 크로매틱 스케일을 다시한 번 살펴보자.

우리가 C음에서부터 출발하여 현의 길이를 2/3을 자르고 가끔씩 두 배로 늘림으로써 F#음까지 7음을 구했고, 반대로 C음에서부터 현의 길이를 3/2로 늘리고 가끔씩 절반으로 자름으로써 D♭음까지 5음을 구해서 총 12음을 얻었다. 자, D♭음에서 한 번 더 피타고라스의 음률을 적용하면 그 음은 G♭음이 될 것이다. 아, 그런데 혹시 다들 기억하는지? 어렸을 때부터 우리가 열심히 익혔던 음악 상식 중 하나는 소위 딴이름한소리 혹은 이명동음(異名同音, enharmonic)라는 개념이었다. 우리의 통상적인 음악 지식 체계 하에서 F#음과 G♭음의 음높이는 동일한 것이며(F#=G♭), 아래 피아노 건반 배열에서 세 개의 검은 건반이 나란히 있는 위치에서 맨 왼쪽 건반이 바로 이 음에 해당한다.

음높이가 동일하다는 것은 그 현에서 발생한 정상파의 진동수가 동일하다는 것을 말한다. 하지만 아래 그림을 자세히 살펴 보자. 피타고라스 음률에서는 F#음과 G♭음이 동일하지 않다(F#≠G♭)! 여기서부터 혼란이 시작된다. 우리가 그간 당연하다고 인식했던 체계가 흔들리는 순간이다.
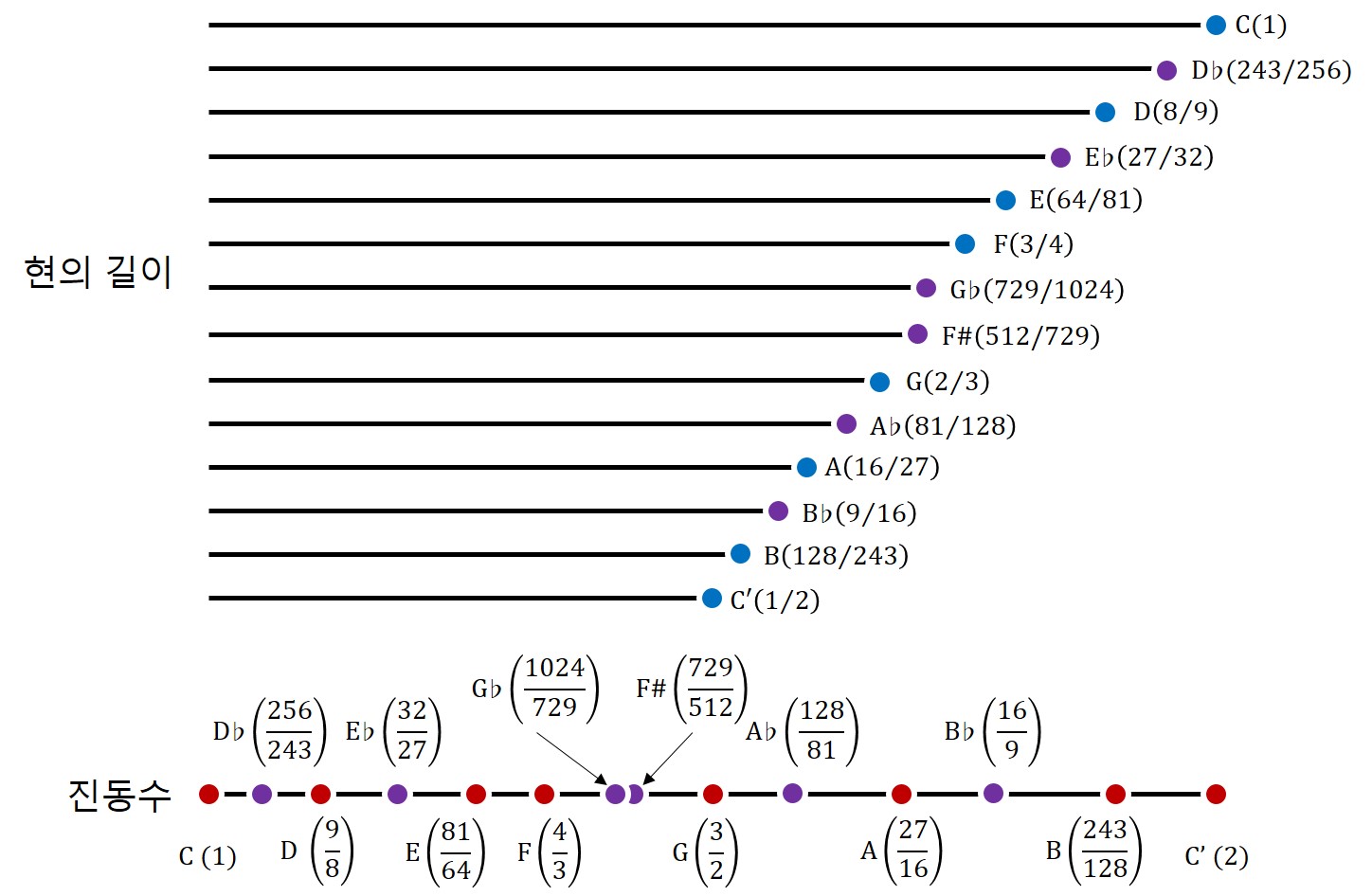
주의 깊게 다시 살펴보자. 우리는 C음에서 피타고라스 음계 찾기 놀이를 한쪽 방향으로 진행했을 때 F#음이 나왔고 그것의 진동수 비율은 729/512(=1.424)였다. 이번에는 반대 방향으로 진행했을 때는 G♭음이 나왔고 그것의 진동수 비율은 1024/729(=1.405)였다. 둘 사이에는 0.019 정도의 차이가 있는데... 문제는 이 두 음정의 차이가 인식 가능할 정도라는 것이다.
가만, 전편에서 우리가 언제 12음계를 얻었는지 기억이 나는가?
| an | 값 | 2에 대한 비율 |
|---|---|---|
| a9 | 1.601806640625 | 80% |
| a10 | 2.4027099609375 | 120% |
| a11 | 1.80203247070312 | 90% |
| a12 | 2.70304870605468 | 135% |
| a13 | 2.02728652954101 | 101% |
우리는 저 101%에 환호작약하며 크로매틱 스케일을 확립했지만 엄밀히 말해 그 값은 정확히는 100%가 아니었다. 진동수 비율을 보면 2.0272865...인데 이것은 2보다 약간 큰 숫자이다. 바로 이 간과했던 차이가 F#음과 G♭음을 서로 다른 음으로 만들어 버리는 원인이 된 것이다. 그런데 이 문제는 유리수만을 수로 취급한 피타고라스 학파에게는 어쩔 수 없는 근본적인 문제였다. 피타고라스 음계 찾는 수열 식을 다시 한 번 살펴보자.
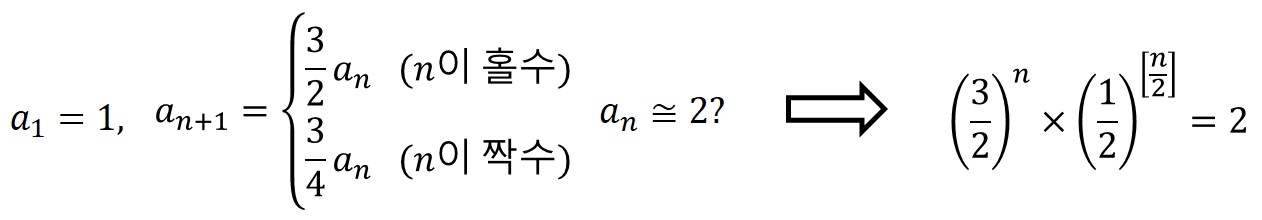
자, 오른쪽 식의 해인 n을 유리수로 표현할 수 있는가? 답은 불가능이다. 지수방정식의 해를 구하기 위해서는 대개 로그(logarithm)를 써야하는데 유리수 전지전능 세계에 살고 있는 피타고라스 학파 사람들이 그런 괴상망측한 더러운(?) 개념을 조화로운 음악에 도입할 리가 없지 않은가. 결국 피타고라스 음률을 통해 조화로운 12음을 얻을 수는 있었으나 완전 5도씩 돌고 돌아서 다니다보니 가장 기본적인 음정 간격이 되는 옥타브가 처음 정의와는 불일치하는 결정적인 문제가 발생하고 말았다. 차이가 나는 진동수 비율인 약 0.027를 소위 피타고라스의 콤마(Pythagorean comma)라고 부른다.
현악기에서는 연주자가 손을 짚는 위치를 미묘하게 바꿈으로서 이 피타고라스의 콤마 문제를 해결할 수가 있었다. 하지만 건반악기는 그것이 불가능했다. 연주 도중에 건반 뚜껑을 열고 렌치를 이용해서 튜닝을 하고 다시 뚜껑을 닫고 '아무 일도 없었다는듯 천연덕스럽게' 연주할 수는 없는 노릇 아니겠는가. 따라서 피타고라스 음률을 이용하여 조율된 건반 악기는 분명 같은 건반 위치인데도 다른 음을 내는 상황이 발생하게 될 것이고 이것은 연주에 큰 문제가 될 수밖에 없었다.
- 1같은 음으로 노래 부르는 것을 제창(齊唱)이라고 하는 것을 상기해보자.
- 2뜬금없는 화학 이야기이지만 화합물 명명시 어떤 구성 원소의 원자 개수가 5개면 바로 이 접두어 '펜타-'를 활용한다. 예를 들면 C5H12 알케인의 영문명은 pentane, PF5의 영문명은 phosphorus pentafluoride.
- 3사실 다이어토닉이라는 단어가 등장하게 된 것은 고대 그리스 음악학에서 다루는 테트라코르돈(τετράχορδoν, tetrachord)이므로 피타고라스 음계 찾기와는 사실 무관한 곳에서 이름이 붙은 것이다. 테트라코르돈 이론에 의하면 완전 4도 간격으로 고정된 두 현 사이에 있는 두 현은 자유롭게 움직여 음높이 조절이 가능한데, 그 방법 중 하나인 디아토니코 게노스(διατονικο γενος, diatonic genes)는 가장 높은 음으로부터 온음-온음-반음의 순서로 구성된 음렬이다. 당시 그리스 사람들은 두 개의 완전 4도 음렬이 온음 간격을 두고 배치되면 옥타브가 되는 것을 알고 있었으므로 두 테트라코르돈을 각각 디아토니코 게노스로 구성하여 음계를 만들었는데, 5개의 온음과 2개의 반음으로 구성되어 있었으므로 이것이 본문에서 설명하는 다이어토닉 스케일과 동일한 것이다. 그러나 테트라코르돈 이론부터 시작해서 음계를 설명하지 않은 이유는, 복잡해서 이해하기 너무 어렵기 때문이다. 테트라코르돈으로 이해하든 피타고라스 음계 찾기 놀이로 이해하든 어쨌든 서양 음악 이론은 이제 통합되었으니 이해하기 쉬운 쪽을 택해서 익혀두면 된다. 참고로 이 테트라코르돈에 관한 주석은 곧 다시 등장할 것이다. (본문에 싣기 부담스러운 것은 주석을 활용하면 되지!)
- 4에포그도온의 문자적인 의미는 '1와 1/8'이라는 뜻이다. 즉 대분수(帶分數)를 읽는 방식이 음의 이름으로 전용된 것이다.
- 5선법의 이름을 부를 때에는 규칙을 정해놓아야 한다. 우선 선법의 이름은 원래 고대 그리스어에서 유래했으므로 다음과 같이 읽어야 하는 것이 정확하다: 이오니아, 도리아, 프리기아, 리디아, 믹솔리디아, 에올리아, 로크리아. 그러나 모드(mode)나 스케일(scale)이라는 단어는 영어 단어이므로 그리스어와 영어를 혼합해서 부를 수는 없는 노릇이니 영어로 통일하는 것이 좋다 (만일 모드나 스케일을 그리스어로 바꿔 부르면 혼란만 가중될 것이다.) 그러니 다음과 같이 읽는다: 아이오니아, 도리아, 프리지아, 리디아, 믹솔리디아, 에이올리아, 로크리아. 그런데 문제는 인도-유럽어족에 속하는 언어들은 명사를 형용사로 바꿀 때 어미의 변화가 일어난다는 점이다. 모두 -a로 끝나는 영단어라서 이 경우 모두 형용사형은 -an이 된다. 따라서 다음과 같이 읽는다: 아이오니안, 도리안, 프리지안, 리디안, 믹솔리디안, 에이올리안, 로크리안. 실제 발음은 [-안]이 아니라 [-언]일 것이다. 하지만 거기까지는 적용하지 않았다. Korean을 [코리안]으로 할지 [코리언]으로 할지는 자유지만 나는 편하게 전자를 택하겠다. 그러니 명칭에 관한 독자들의 혼란이 없기를 바라며!
- 6테트라코르돈 이론에서 크로마티코 게노스(χρωματικο γενος)는 가장 높은 음으로부터 낮은 음까지의 완전 4도가 단3도(온음+반음 음정 간격, 곧 1.5음)-반음-반음의 순서로 구성된 음렬이다. 그런데 디아토니코 게노스가 다이어토닉 스케일과 어느 정도 연관이 있는 반면, 크로마티코 게노스는 크로매틱 스케일과는 사실 큰 관련이 없다. 다만, 다이어토닉이 아닌 것에 대응된다는 점과 반음이 더 많이 사용된다는 점에서 아마 크로매틱 스케일이라는 이름이 붙여진 듯 하다.
- 7B♭는 항상 쓰이는 음은 아니었고 필요에 의해 B 대신에 쓰이곤 했는데, 그 이유는 6편에 나오는 악마의 음정인 셋온음(tritone) 때문이었다.
- 8쇼팽의 연습곡은 그 자체로도 훌륭한 연주곡 소품으로 인정받을 정도로 놀라운 짜임새와 기교를 자랑한다. 그래서 그런 간단한 '연습을 위한 곡' 정도로 생각하는 것은 큰 오산이다.
▲[이전글] 4. 피아노 현 (Piano Strings)
▼[다음글] 6. 평균율과 불협화음 (Equal Temperament and Dissonance)
 |
이 저작물은 크리에이티브 커먼즈 저작자표시-비영리-동일조건변경허락 4.0 국제 라이선스에 따라 이용할 수 있습니다. |